[プレスリリース] 研究成果発表(伊藤一般教養部講師)
新たな結び目理論で「微分」の概念を刷新
—圏論化による結び目ホモロジーで量子論への更なる応用が期待—
本校教員と東大研究員のペア、20年の沈黙を破る結果を出す
2020年6月24日

独立行政法人国立高等専門学校
茨城工業高等専門学校
【概要】
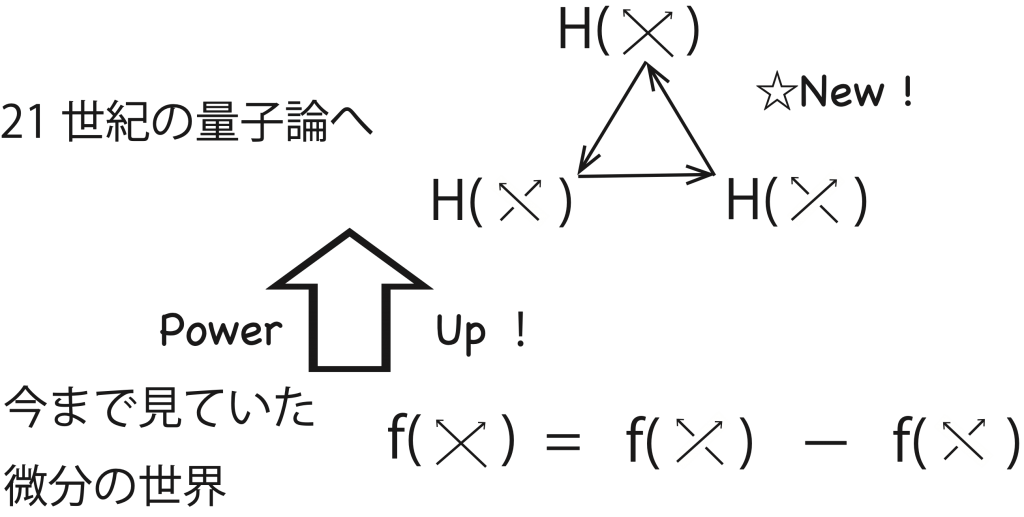
紐全体の構造を調べるのに有効な微分理論が21世紀の量子論に対応して、どのように観察・観測されるかあらゆる科学で知られていませんでした。ところが、それは量子次数というものを動かさない「紐の交差交換[mfn]「紐の接ぎ替え」の項を参照のこと。[/mfn]」(紐の接ぎ替え[mfn]2つの紐を使って机などに十字を重ねて交差を作るとき、この交差1つに対して、交差をなす紐の上下を接ぎ替えにより入れ替えることを専門用語で「交差交換」という。言い換えるなら、紐の接ぎ替え、である。[/mfn])における空間列だということを、今回、数学によって初めて突き止め(図1の三角構造)、さらには物理量となる新しい「結び目ホモロジー [mfn]結び目の関数が、結び目を入力すると数を値としてとるのに対し、結び目のホモロジー群は結び目を入力すると、「数の空間」を返す。数の空間は、通常は整数全体の集合をいくつか組みにしたもので記述される。「ホモロジー」の項目で説明したように、結び目ホモロジーは、結び目の幾何的な特徴を捉える。本論文では結び目ホモロジーの新しい組み上げ構造を考案し、結び目よりも広い対象の新しいホモロジーを世の中に与えた。[/mfn] 」を発見しました(図1の「H」)。
【このリリースのポイント】
(1) 科学では重要な「紐の空間構造」を調べるため20世紀では「結び目 [mfn] 閉じた1本の紐のこと。物理学、化学、生物学に現れる。直接紐になっていなくても飛行機の翼端の渦や宇宙空間の交差空間を結び目だということもある。日本では高分子やDNAにおける結び目理論研究が活発である。 [/mfn] の関数や微分」が使われてきた。
(2) 21世紀、圏論 [mfn] 数学の基礎を相対的な関係性により定義・構築し、考えている数学の容れ物と自分が考えている立場を明確に記述することを可能にする、数学の一分野。考察している2つの数学を有効に関連付け、互いの数学に応用することができる。 [/mfn] 化と呼ばれる手法により結び目の関数を統制する「結び目ホモロジー」が発見された。
(3) 今回、21世紀の方法により20世紀的な「紐の微分理論」がどのように捉えられるかを数学によって初めて
突きとめた。
数学におけるカテゴリフィケーションの具体例として近年最も注目を浴びたものが、ジョーンズ多項式[mfn]1984年頃に作用素環論と呼ばれる分野から見出された結び目不変量。ジョーンズ(1990年にフィールズ賞受賞)が発見した。なお、結び目量子不変量として、またスケイン関係式により再定式化がなされ、量子パラメータを変数として持つ。[/mfn]のカテゴリフィケーションと呼ばれるものである。これはホバノフ(Khovanov, 現コロンビア大学教授)により2000年に発表され大きな波及効果があった。特に以下のメリットが知られている。
■ 結び目のジョーンズ多項式を純粋に一般化している様子がわかりやすい。
■ 分野横断的によく用いられるフロベニウス(Frobenius)代数と対応する (1+1) TQFT(位相的場[mfn]量子論によれば、空間内を飛び回る粒子は、空間内に広がる「状態」とみなされる。このような設定を数学公理系として記述したもの(1966年のフィールズ賞受賞者のアティヤによる)が位相的場の理論である。「状態」を捉える空間を時間発展させた、より広い空間(専門用語では「コボルディズム」)を数学で扱えるようになる。本論文ではこの理論が駆使された。[/mfn]の量子論, Topological Quantum Field Theory)を使って構成されており扱いやすい。
■ はっきりとした応用がある。物理学–より洗練化されたチャーン・サイモンズ理論のモデルや真空状態の記述。数学–ジョーンズ多項式で区別できないペアを区別する / ミルナー予想の簡易な別証明。(今回の関連では、量子コンピューティングへの応用として伊藤昇の2011年のホバノフホモロジー[mfn]2000年頃にホバノフが発見した。ジョーンズ多項式を量子パラメータの次数ごとに整理したとき、各係数をオイラー数とするようなホモロジー群が対応する上部構造を持たせる仕組み。このホモロジー群は結び目不変量となっている。[/mfn]に関する論文(N.Ito, 2011)が量子符号理論に活用 (Audoux, 2014)されている。)
「結び目の交差交換」という基本的で汎用性が高い幾何的な手術、「紐の局所的な交差交換」(図1左)は、結び目の複雑さを測る上での重要な古典的不変量である「結び目解消数」を定義するだけでなく、結び目量子不変量 [mfn] 量子群と呼ばれる、量子化された空間の構造を用いて作られた結び目不変量のこと。なお、量子群は神保道夫とドリンフェルトにより、独立に発見された。また、ドリンフェルトは1990年のフィールズ賞受賞者。 [/mfn] のスケイン関係式[mfn] 関数f、交差交換1つに対し、次の形の関係式のことをいう。
f(上になった紐の状態) – f(下になった紐の状態) = f(中途状態の特異結び目).
一般にスケイン関係式というときは、上記のような形(3項であるとか単純な引き算)とは限らず、また「中途状態」を用いず結び目/絡み目だけで構成されるものを指すことが多い。本論文ではバシリエフのスケイン関係式に背後構造が付加され、新たな意味付けがなされた。言い換えるなら、本論文でこの関係式が世界で初めて圏論化された。
[/mfn](量子群におけるR-行列の差によって導かれるもの)を記述するものとしても重要です。中でもバシリエフ (Vassiliev)不変量のスケイン関係式やアレクサンダー・コンウェイ(Alexander-Conway)多項式は交差交換の単純な差により記述されます(今回の論文でのバシリエフ不変量 [mfn]本論文の主役の1つ。結び目全体がなす集合を、特異結び目を使い分類する仕組みを持つ「不変量のタイプ」(バシリエフ型と呼ばれる)のことを指し、具体的な結び目不変量とは一線を画す。バシリエフ型であることは、バシリエフスケイン関係式(本論文が圏論化した関係式)を使って確かめられる。異なる結び目の量子不変量であっても、量子パラメータの「微分によって正規化」すると係数にバシリエフ不変量が現れる。この普遍性が有名である。関数として計算効率が良いことでも知られる。関数の微分による正規化は高専2年で習う。 [/mfn] のスケイン関係式は図1右)。
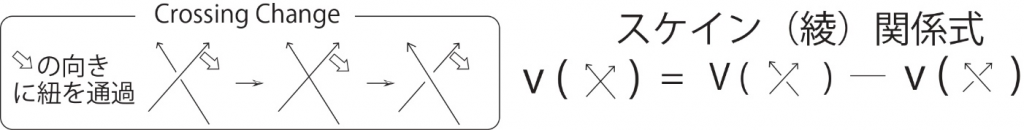
図1
特に結び目量子不変量の量子パラメーターqのテーラー展開の各次係数はどれもVassiliev不変量になっています。このことにより量子群を司るリー(Lie)代数に依存しないという意味で、Vassiliev不変量は普遍的です。
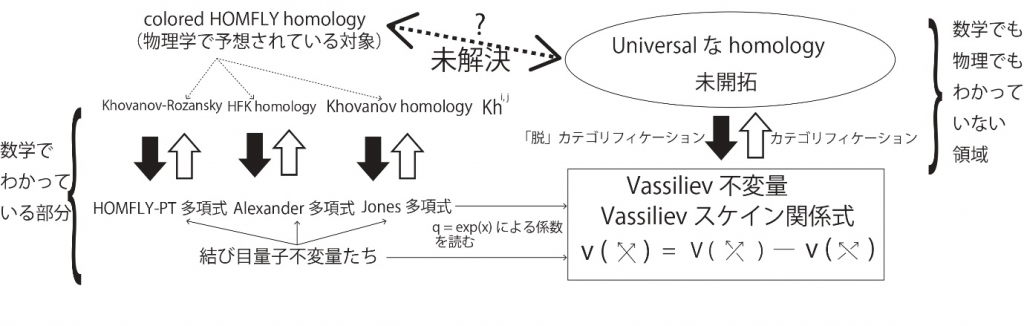
図2
【背景】
現在、カテゴリフィケーション [mfn]厳密な数学的な定義はなく数学の上部構造を表すキーワード。例えば1 、2 、3に対し1次元空間、2次元空間、3次元空間の列を想起し、元は単に「3つの数」であったものに深い意味や構造を持たせること。本論文の主役の一つである。 [/mfn] という考え方は多方面の数学で有効であることが広く知られています((深谷,2016)および「チャーン賞柏原正樹氏が受賞」(『日経サイエンス』,2018年10月号))。そして実際にカテゴリフィケーション を応用する研究は今や世界的にとても多いことが事実としてあります。しかし一方で、その波及効果とは裏腹に、有効なカテゴリフィケーションをするのは難易度が高いことも知られています。それ故、ホバノフ理論が始まってから20年を経ても1990年代のバシリエフ理論と2000年代のホバノフ理論を有機的に結びつけて活用することができずにいました。
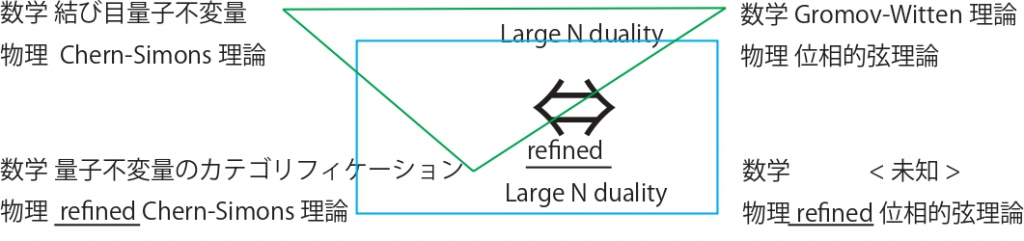
図3(亀山.2017)に基づく。
【今回の成果】
本研究ではホバノフホモロジー上で「結び目の交差交換」を実現し、バシリエフのスケイン関係式における引き算を回復し長完全列を内包するホバノフホモロジーに拡張しました。交差交換を与えるホバノフ複体(complex)上の写像(列)は位相的な不変性を満たし特異結び目(singular link) [mfn] 交差交換が行われる2つの結び目同士の「中間体」に相当するもの。局所的に一方の紐が他方の紐を横断するときに現れる2重点(特異点)をもつ。 [/mfn] のホバノフホモロジーを導きます。このホモロジー [mfn] 数学の各分野に登場する概念。大学3, 4年では、幾何形状を調べる道具として導入される。調べたい空間を分割し、各パーツの境界による関係性を数学的に書き上げることで(たとえ想像が難しいものでも)幾何形状の特徴を捉えることができる。専門用語では「関手」と呼ばれる空間同士の組織的な対応づけの道具にもなっている。 [/mfn] はコンツェビッチ(Kontsevich) の普遍積分 [mfn] バシリエフ不変量をひとまとめに表したものに相当する積分をいう。ここにも特異結び目が満たすFI関係式が現れる。コンツェビッチは1994年のフィールズ賞受賞者。なお、本論文では圏論化したFI関係式を世界で初めて記述した。 [/mfn] に現れるFI 関係式を満たし、非自明であることが保証されます。この構成物からジョーンズ多項式の情報は全て回復します。なお、伊藤の調べた限りでは、このような微分の次数も応用できるような、特異結び目へ拡張がなされたホバノフホモロジーは初めてとなります。
以上から結び目を 調べることに用いられてきた20世紀的な「微分」は、「紐の交差交換」におけるホモロジー完全系列 [mfn] ホモロジーは次数という整数を持ち、幾何学的な空間形状をより分析的に捉えられる。調査したい空間が、さらに別の2つ空間対との関係性により、分析できる場合、3つ組の空間対を念頭において、ホモロジー完全列という、ホモロジー群の列が存在し、私たちに豊かな空間情報を提供する。本論文では新しいホモロジー完全(系)列を世の中に与えた。 [/mfn] だということが今回数学によって初めて探し当てられ、証明されたことになります。
【応用上のポイント】
(1) 発見されたホモロジーは今までにない性質を持つことが数学で証明された。
(2) 物理学における場の理論、量子コンピュータ、化学、生物学への応用が期待される。

「写真提供:数学セミナー編集部」
【研究費へのコメント(代表者 伊藤昇)】
この春、科学技術研究費補助金(研究課題番号20K03604)による研究もスタートしました。
研究課題名:「バシリエフ不変量の圏論化の探求と展開」、
研究代表者:伊藤昇(茨城高専)、研究分担者:初田真知子(順天堂大学)、吉田純(東京大学)。
この研究を強力に推進していきたいと思っています。
【共著者:吉田純氏(東京大学)のコメント】

「写真提供:CT2017」
【本論文の問題を解いた時の黒板写真】

<プレリリース英語要約>
In this paper, we obtain a categorified version of Vassiliev skein relation on Khovanov homology. More precisely, we show that a genus-one operation on TQFT gives rise to a crossing change on Khovanov complexes. The invariance under Reidemeister moves turns out, and it enables us to extend Khovanov homology to singular links. We then see that its long exact sequence categorifies Vassiliev skein relation for the Jones polynomials. We also obtain the categorified FI relation.
【論文情報】
★論文タイトル:Crossing change on Khovanov homology and a categorified Vassiliev skein relation (arXiv:1911.09308, with Jun Yoshida)
URL: https://www.worldscientific.com/doi/abs/10.1142/S0218216520500510
★ジャーナル名:Journal of Knot Theory and Its Ramifications
URL: https://www.worldscientific.com/worldscinet/jktr
著者:伊藤 昇, 吉田 純
【参考文献情報】
Noboru Ito, “Chain homotopy maps for Khovanov homology”, Journal of Knot Theory and Its Ramifications, 2011, 20(1), pp127-139.
深谷賢治,ゲージ理論とシンプレックティック幾何学における不変量のカテゴリー化について,第17回高木レクチャー招待講演(2016年6月),京都大学,オンラインURL:https://www.ms.u-tokyo.ac.jp/~toshi/jjm/JJMJ/JJM_JHP/contents/takagi_jp/17th/TL-Fukaya_jp.html(参照2020年5月19日)
日経サイエンス,“チャーン賞を柏原正樹氏が受賞”,日経サイエンス2018年10月号, http://www.nikkei-science.com/?p=57088,(参照2020年5月19日)
亀山昌也,「LMOV 予想とその精密化」,研究集会「結び目の数学X」報告集(2017), オンラインURL: http://www.math.twcu.ac.jp/mok10/proc/15Kameyama.pdf ,(参照2020年5月19日)
CT2017(International Category Theory Conference 2017)(2017年7月), Canada, オンラインURL: http://www.mat.uc.pt/~ct2017/ ,(参照2020年5月19日)
【本件に関する問い合わせ先】
茨城工業高等専門学校 国際創造工学科 一般教養部 講師
伊藤 昇(いとう のぼる)
Tel: 029-272-5201/029-271-2614(研究室直通)
E-mail: nito★ibaraki-ct.ac.jp(★を@に変換願います。)
(報道について)
茨城工業高等専門学校 総務課 研究協力・地域連携係
Tel: 029-271-2952
E-mail:kenkyo★sec.ibaraki-ct.ac.jp(★を@に変換願います。)


