[プレスリリース] 研究成果発表(伊藤一般教養部講師)
【交代結び目における日本人の快挙】
メビウスの帯のつかまえかた
—結び目膜の表裏をかぞえる等式を62年ぶりに証明—
2020年11月20日
独立行政法人国立高等専門学校機構
茨城工業高等専門学校
学習院中等科


[su_heading size=”24″ align=”left” margin=”90″]発表概要[/su_heading]
茨城工業高等専門学校の伊藤昇教員,学習院中等科の瀧村祐介教諭(数学)は,交代結び目について張られる膜のうち「表裏が付かない場合」について新しい等式を発見し,証明しました.
1958年に村杉邦男先生(トロント大学名誉教授)が,衣服を縫うように上下に結って閉じた紐に張られる膜のうち「表裏が付く場合」についてその形を決定しました.しかし「表裏が付かない場合」は未解決問題として長い間残っていました.
今回その「表裏が付かない場合」の問題を本校の伊藤昇教員(国際創造工学科 一般教養部)が1958年以来,62年ぶりに大きく進展させ,新しい等式を発見し証明しました.その論文は2020年9月22日に受理されました(International Journal of Mathematics).
2016年に伊藤教員と共に平面に描かれる曲線を研究していた瀧村祐介教諭(学習院中等科)の研究結果と三次元の膜に隠れているメビウスの帯の個数とを伊藤教員が見比べてみたところ,見れば見るほどに驚くほど一致していることに気づいたことが解決の端緒となったとのことです.最初に明らかになった結果を論文にまとめ発表したことで,今度は海外の研究者との息の詰まるような競争が始まり,いつ誰かが完全な証明をしてしまうのではないかと,この4年間は気が気ではなかったそうです.
海外勢からの重圧にさらされる一方,日本の研究者からは情報提供や助言といったあらゆるサポートを受けることができ,何とか証明までこぎつけたとのことでした. 今回の解決は研究の完結ではなく,物理や工学への展開に繋がったり,計算方法など実装へ展開したり,また生物学や化学などへの新たな応用も期待されます.
(報道機関へのプレスリリースについてはこちらをご覧ください)
[su_heading size=”24″ align=”left” margin=”90″]伊藤教員へのインタビュー[/su_heading]
― 本校国際創造工学科 一般教養部 伊藤 昇(いとう のぼる)先生に,今年の9月22日に受理された論文について伺いたいと思います.今回62年ぶりの大きな進展が見られたということですが,まず,どのようなものが懸案の問題であったのかをお聞かせください.
伊藤教員(以下,伊):一言で言いますと,新しい等式を作りました.まず,空間内の紐がミクロからマクロまで様々な科学において必須なものであることはよく知られており,19世紀以前から重要視されていました.
例えば関係する研究者としてケルビンやガウスといった歴史上有名な科学者があがります.それでは閉じた紐「結び目」の複雑さの指標として何が候補として考えられるでしょうか? もっとも由緒正しいものの一つとして石鹸膜のように曲面を張り,「曲面の複雑さ」として説明する方法があります.

これは1930年代には研究され知られておりました.したがいまして,この複雑さを決める,という問題がこの100年間耳目を集めていたということになります.これは空間内の紐を数学として取り扱うなら,最初に考える問題の一つと言っても過言ではないでしょう.
― 62年前にはどのようなことがあったのでしょうか.
伊:閉じた紐に張られる,表裏がつく曲面の複雑さについて村杉邦男先生が素晴らしい等式を発見しました.表裏がある曲面は1人乗りの浮き輪,2人乗りの浮き輪のように穴がいくつあるかで判定しようということになるのですが,衣服を縫うように上下に結って閉じる紐「交代結び目」について村杉先生は,その穴の数を全て決定しました.1959年のCrowellの論文も同時期に同じ結果を出した論文として有名です.
― そういった背景がある中,伊藤先生が今回どのような結果を出されたのでしょうか.
伊:村杉先生の考えた結び目たちに対して,表裏が付かない場合が未解決でしたが,新しい等式を証明し,発見しました.
― どうやって突破口を掴まれたのでしょうか?
伊:ある時,瀧村先生に問題を投げかけました.「空間内の紐をほどく指標は有名ですが,平面上に描かれる曲線に対して同様の指標は与えられますか?」といったような質問です.すると瀧村先生はしばらくたって次のような列から始まる表を持ってこられました.
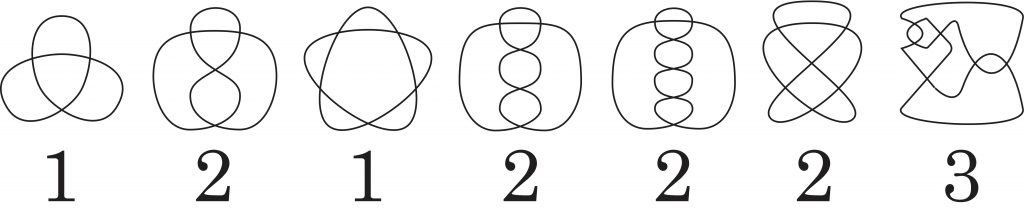
しばらく,この表を眺めていると何か意味(ルール)があるのではないかと思うようになったのです.そうして2つの表を見比べると,それは衝撃でした.「最低いくつのメビウスの帯が含まれているか」という数の表とそっくりだったのです!
― 研究をされる中で,海外との競争はありましたでしょうか.
伊:数学は国際交流がすごく盛んな分野ですので,当然ながら,ありました.いつ誰かに解かれるのではないかと冷や冷やしながら,強いプレッシャーやストレスを感じながらの研究となりました.
― 日本人研究者との競争もあったのでしょうか.
伊:本来だったら,あるはずのものなのですが,今回は日本の先生が全員味方をしてくださいました.「これが役に立つのでは」「こういう定義がいいのではないか」「こういう考え方がよいのではないか」とレストランや喫茶店で助言をくださったり,手に入りにくい修士論文を譲ってくださったり,研究集会で進展を述べるたびに足りない点を優しくご指摘くださったりと,実に様々な形でサポートして下さいました.それが大変励みとなりました.数学はガウスやリーマン,岡潔といった大天才が個人で解くイメージがありますが,21世紀に入り,研究者たちが協力し合う形に変わってきていることは既に専門家が指摘しています.今回は,まさに力を総結集した結果となりました.年長の先生が助けてくれなければ,問題が解けたタイミングはもっと遅くなっていたことでしょう.
― そうして研究を進めていく中で,「おっ,この問題は解けそうだな」というのはどういった感覚なのでしょうか.
伊:その感覚を表現するのは難しいのですが,少しずつ述べてみましょう.今回の場合ですとまず表を見比べた時に感じた「驚き」の対応がありました.しかし,ルールがあるような気がずっとしていたのです.数学の発見をするときは,パッと閃く人もいることは知っておりますが,私は地道に詰めていくタイプなので,直観からすれば半信半疑に思えるようなことを,ひたすら論理を用いて詰めていく作業をしていきます.このように論理的に詰める作業を継続していくと,それが直観に変わってきます.しばらくすると,「ああ,これは成り立って然るべきなのではないか」,そう思える時点が訪れます.それこそが「解けるかな」が「解けそうだな」という確信に変わる瞬間です.
― 今回の論文を世に出したことで,他の研究者の反応はいかがでしょうか.
伊:海外からの反響はあります.そのスピード感に驚くばかりです.瀧村先生の表から私が曲面のメビウスの帯を見出したという論文 (https://www.worldscientific.com/doi/10.1142/S0129167X18500842) を受けて,海外では三次元の幾何学の方法を使って二次元を表現するという,ちょうど私と真逆の方法で今回の問題の解決がなされました ( 参考YouTube:https://www.youtube.com/watch?v=L6gCoOUnrgE&feature=youtu.be) .そして他の先生方は計算テクニックについてどんどん開発しておられます.
― 今回の発見でひと段落ということではないのですね.既に次の展望というものはお持ちでしょうか.
伊:今回の等式は,ある状況においては「三次元のトポロジーが二次元で決まる」という意味を指しています.もっといえば,「数が形を決定している」ことを表しているとも言えます.ですが,意味はそれだけではありません.1984年にジョーンズ多項式というものが見つかりまして,そのジョーンズ先生はそれでフィールズ賞を受賞されたのですが,今回の新等式はそのジョーンズ多項式の係数と深い関係があることがわかっています.したがいまして,そういった量子物理の展開とつながっているのではないかというところが期待されます(参考URL:/info/archives/24436).もう一つの重要な視点としては,その計算方法の開発です.空間曲線に対して複雑さを計算できることになりますので,ありとあらゆる空間曲線を入力すると,それに張られる膜のメビウスの帯数が出力される関数を手にすることになります.これは面白い展開があるように予感します.茨城高専はアルゴリズムの実装に強いので,情報分野の専門家である米倉校長先生のアドバイスを受けつつ,学生さんたちと議論をして進めていきたいとおもっております.あとは幾何学的な展開ですね.3次元幾何学,3次元トポロジーの中で今まで明らかになっていなかったことが可視化され,皆さんが理解しやすい理論に育っていくようにも思えます.
― 令和2年度(独立行政法人国立高等専門学校機構)研究プロジェクト経費助成事業・研究ネットワーク形成支援事業の採択を受けての今後の決意をお聞かせ願えますか?
伊:恩師であるViro 先生の結果 (2004)と私の結果(2011)が海外で量子情報に応用されたことがありまして,その発展と実装を考えるのがこの研究費における目的です.理論から応用,応用から実装といった方向で積極的に研究を進めていきたいです.
あまり知られてないことですが国立高専全体の科研費獲得件数は医薬を持たない機関で比べると全国でトップ3だと言われています.すなわち一つ一つは大きくなくとも,皆で束になれば,大きな力になるはずなのです.

今回,オールジャパンの布陣を引くために石川高専の小林竜馬先生,阿南高専の浮田卓也先生に加えて,大山口菜都美先生(秀明大/東大情報学環),吉田純先生(東工大/東大数理)に構成員として入っていただきました.今後,研究のネットワークを拡げる努力をして,再び皆様のお力をお借りして少しでも大事なことが研究でき,また新たな成果を生み出していけたら,と思います.
― 本日は興味深いお話をどうも有難うございました.
<瀧村教諭のコメント>
今回の研究は,球面上の結び目の影(knot projection)の研究から発展し,空間内の結び目(knot)へ応用されたものである.この結果をもとに,素な交代結び目(prime alternating knot)に限らず,一般の結び目のcrosscap number の研究が発展されることを期待している.[su_heading size=”30″ align=”left” margin=”90″]学生による伊藤先生への質問動画 ~教えて!伊藤先生~ [/su_heading]
本科1年生の学生3名が、伊藤先生に今回の研究成果について質問してきました。
動画「教えて!伊藤先生」は、「茨城高専公式YouTubeチャンネル」からご覧いただけます。
(リンクはこちら→ https://www.youtube.com/watch?v=D43rtzuvaUk)
【本件に関する問い合わせ先】
茨城工業高等専門学校 国際創造工学科 一般教養部 講師
伊藤 昇(いとう のぼる)
Tel: 029-272-5201/029-271-2614(研究室直通)
E-mail: nito★ibaraki-ct.ac.jp(★を@に変換願います。)
(報道について)
茨城工業高等専門学校 総務課 研究協力・地域連携係
Tel: 029-271-2952
E-mail:kenkyo★sec.ibaraki-ct.ac.jp(★を@に変換願います。)


